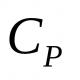• Palitan ang mga positibong halaga ng numero sa function x (\displaystyle x) at kaukulang mga negatibong numerong halaga. Halimbawa, ibinigay ang function f (x) = 2 x 2 + 1 (\displaystyle f(x)=2x^(2)+1). Palitan ang mga sumusunod na halaga dito x (\displaystyle x):

Suriin kung ang graph ng function ay simetriko tungkol sa Y axis. Ang simetrya ay nangangahulugang isang salamin na imahe ng graph na may kaugnayan sa ordinate. Kung ang bahagi ng graph sa kanan ng Y-axis (mga positibong halaga ng independent variable) ay pareho sa bahagi ng graph sa kaliwa ng Y-axis (negatibong mga halaga ng independent variable ), ang graph ay simetriko tungkol sa Y-axis Kung ang function ay simetriko tungkol sa y-axis, ang function ay pantay.

Suriin kung ang graph ng function ay simetriko tungkol sa pinagmulan. Ang pinagmulan ay ang puntong may mga coordinate (0,0). Symmetry tungkol sa pinagmulan ay nangangahulugan na ang isang positibong halaga y (\displaystyle y)(na may positibong halaga x (\displaystyle x)) ay tumutugma sa isang negatibong halaga y (\displaystyle y)(na may negatibong halaga x (\displaystyle x)), at kabaliktaran. Ang mga kakaibang function ay may simetrya tungkol sa pinagmulan.

Na pamilyar sa iyo sa isang antas o iba pa. Nabanggit din doon na ang stock ng mga katangian ng pag-andar ay unti-unting mapupunan. Dalawang bagong pag-aari ang tatalakayin sa seksyong ito.

Kahulugan 1.

Ang function na y = f(x), x є X, ay tinatawag kahit na para sa anumang halaga x mula sa set X ang pagkakapantay-pantay ng f (-x) = f (x).

Kahulugan 2.

Ang function na y = f(x), x є X, ay tinatawag na kakaiba kung para sa anumang halagang x mula sa set X ang pagkakapantay-pantay ng f (-x) = -f (x).

Patunayan na ang y = x 4 ay isang even function.

Solusyon. Mayroon kaming: f(x) = x 4, f(-x) = (-x) 4. Ngunit(-x) 4 = x 4. Nangangahulugan ito na para sa anumang x ang pagkakapantay-pantay na hawak ng f(-x) = f(x), i.e. pantay ang function.

Katulad nito, mapapatunayan na ang mga function na y - x 2, y = x 6, y - x 8 ay pantay.

Patunayan na ang y = x 3 ~ isang kakaibang function.

Solusyon. Mayroon kaming: f(x) = x 3, f(-x) = (-x) 3. Ngunit (-x) 3 = -x 3. Nangangahulugan ito na para sa alinmang x ang pagkakapantay-pantay na hawak ng f (-x) = -f (x), i.e. kakaiba ang function.

Katulad nito, mapapatunayan na ang mga function na y = x, y = x 5, y = x 7 ay kakaiba.

Ikaw at ako ay nakumbinsi nang higit sa isang beses na ang mga bagong termino sa matematika ay kadalasang may "makalupang" pinagmulan, i.e. maipaliwanag sila kahit papaano. Ito ang kaso sa parehong pantay at kakaibang mga pag-andar. Tingnan ang: y - x 3, y = x 5, y = x 7 ay mga kakaibang function, habang ang y = x 2, y = x 4, y = x 6 ay even functions. At sa pangkalahatan, para sa anumang function ng form na y = x" (sa ibaba ay partikular nating pag-aaralan ang mga function na ito), kung saan ang n ay isang natural na numero, maaari nating tapusin: kung ang n ay isang kakaibang numero, kung gayon ang function na y = x" ay kakaiba; kung ang n ay isang even na numero, kung gayon ang function na y = xn ay even.

Mayroon ding mga function na hindi kahit na o kakaiba. Ganito, halimbawa, ang function na y = 2x + 3. Sa katunayan, f(1) = 5, at f (-1) = 1. Gaya ng makikita mo, dito, samakatuwid, ni ang pagkakakilanlan f(-x) = f ( x), o ang pagkakakilanlan f(-x) = -f(x).

Kaya, ang isang function ay maaaring maging kahit na, kakaiba, o hindi.

Ang pag-aaral kung ang isang binigay na function ay even o odd ay karaniwang tinatawag na pag-aaral ng parity.

Ang mga kahulugan 1 at 2 ay tumutukoy sa mga halaga ng function sa mga puntos na x at -x. Ipinapalagay nito na ang function ay tinukoy sa parehong point x at point -x. Nangangahulugan ito na ang point -x ay kabilang sa domain ng kahulugan ng function na kasabay ng point x. Kung ang isang numerical set X, kasama ang bawat isa sa mga elemento nito x, ay naglalaman din ng kabaligtaran na elemento -x, kung gayon ang X ay tinatawag na isang simetriko set. Sabihin nating, (-2, 2), [-5, 5], (-oo, +oo) ay simetriko set, habang \).

Dahil \(x^2\geqslant 0\) , ang kaliwang bahagi ng equation (*) ay mas malaki kaysa o katumbas ng \(0+ \mathrm(tg)^2\,1\) .

Kaya, ang pagkakapantay-pantay (*) ay masisiyahan lamang kapag ang magkabilang panig ng equation ay katumbas ng \(\mathrm(tg)^2\,1\) . At ito ay nangangahulugan na \[\begin(cases) 2x^2+\mathrm(tg)^2\,1=\mathrm(tg)^2\,1 \\ \mathrm(tg)\,1\cdot \mathrm(tg)\ ,(\cos x)=\mathrm(tg)^2\,1 \end(cases) \quad\Leftrightarrow\quad \begin(cases) x=0\\ \mathrm(tg)\,(\cos x) =\mathrm(tg)\,1 \end(cases)\quad\Leftrightarrow\quad x=0\] Samakatuwid, ang value na \(a=-\mathrm(tg)\,1\) ay nababagay sa amin.

Sagot:

\(a\in \(-\mathrm(tg)\,1;0\)\)

Gawain 2 #3923

Antas ng gawain: Katumbas sa Pinag-isang Pagsusulit ng Estado

Hanapin ang lahat ng mga halaga ng parameter \(a\) , para sa bawat isa kung saan ang graph ng function \

simetriko tungkol sa pinagmulan.

Kung ang graph ng isang function ay simetriko tungkol sa pinanggalingan, kung gayon ang naturang function ay kakaiba, iyon ay, \(f(-x)=-f(x)\) hold para sa anumang \(x\) mula sa domain ng kahulugan ng function. Kaya, kinakailangan upang mahanap ang mga halaga ng parameter kung saan \(f(-x)=-f(x).\)

\[\begin(aligned) &3\mathrm(tg)\,\left(-\dfrac(ax)5\right)+2\sin \dfrac(8\pi a+3x)4= -\left(3\ mathrm(tg)\,\left(\dfrac(ax)5\right)+2\sin \dfrac(8\pi a-3x)4\right)\quad \Rightarrow\quad -3\mathrm(tg)\ ,\dfrac(ax)5+2\sin \dfrac(8\pi a+3x)4= -\left(3\mathrm(tg)\,\left(\dfrac(ax)5\right)+2\ kasalanan \dfrac(8\pi a-3x)4\kanan) \quad \Rightarrow\\ \Rightarrow\quad &\sin \dfrac(8\pi a+3x)4+\sin \dfrac(8\pi a- 3x)4=0 \quad \Rightarrow \quad2\sin \dfrac12\left(\dfrac(8\pi a+3x)4+\dfrac(8\pi a-3x)4\right)\cdot \cos \dfrac12 \left(\dfrac(8\pi a+3x)4-\dfrac(8\pi a-3x)4\right)=0 \quad \Rightarrow\quad \sin (2\pi a)\cdot \cos \ frac34 x=0 \end(aligned)\]

Ang huling equation ay dapat masiyahan para sa lahat ng \(x\) mula sa domain ng \(f(x)\), samakatuwid, \(\sin(2\pi a)=0 \Rightarrow a=\dfrac n2, n\in\mathbb(Z)\).

Sagot:

\(\dfrac n2, n\in\mathbb(Z)\)

Gawain 3 #3069

Antas ng gawain: Katumbas sa Pinag-isang Pagsusulit ng Estado

Hanapin ang lahat ng value ng parameter \(a\) , para sa bawat isa kung saan ang equation \ ay mayroong 4 na solusyon, kung saan ang \(f\) ay isang periodic function na may period \(T=\dfrac(16)3\) tinukoy sa buong linya ng numero , at \(f(x)=ax^2\) para sa \(0\leqslant x\leqslant \dfrac83.\)

(Gawain mula sa mga subscriber)

Dahil ang \(f(x)\) ay pantay na function, ang graph nito ay simetriko na may kinalaman sa ordinate axis, samakatuwid, kapag \(-\dfrac83\leqslant x\leqslant 0\)\(f(x)=ax^2\) . Kaya, kapag \(-\dfrac83\leqslant x\leqslant \dfrac83\), at ito ay isang segment ng haba \(\dfrac(16)3\) , function \(f(x)=ax^2\) .

1) Hayaan \(a>0\) . Pagkatapos ang graph ng function na \(f(x)\) ay magiging ganito:


Pagkatapos, upang ang equation ay magkaroon ng 4 na solusyon, kinakailangan na ang graph \(g(x)=|a+2|\cdot \sqrtx\) ay dumaan sa puntong \(A\) :


Kaya naman, \[\dfrac(64)9a=|a+2|\cdot \sqrt8 \quad\Leftrightarrow\quad \left[\begin(gathered)\begin(aligned) &9(a+2)=32a\\ &9(a +2)=-32a\end(aligned)\end(gathered)\kanan. \quad\Leftrightarrow\quad \left[\begin(gathered)\begin(aligned) &a=\dfrac(18)(23)\\ &a=-\dfrac(18)(41) \end(aligned) \end( natipon)\tama.\] Dahil ang \(a>0\) , kung gayon ang \(a=\dfrac(18)(23)\) ay angkop.

2) Hayaan \(a<0\) . Тогда картинка окажется симметричной относительно начала координат:


Kinakailangan na ang graph \(g(x)\) ay dumaan sa puntong \(B\) : \[\dfrac(64)9a=|a+2|\cdot \sqrt(-8) \quad\Leftrightarrow\quad \left[\begin(gathered)\begin(aligned) &a=\dfrac(18)(23 )\\ &a=-\dfrac(18)(41) \end(aligned) \end(gathered)\kanan.\] Mula noong \(a<0\) , то подходит \(a=-\dfrac{18}{41}\) .

3) Ang kaso kapag ang \(a=0\) ay hindi angkop, mula noon \(f(x)=0\) para sa lahat ng \(x\) , \(g(x)=2\sqrtx\) at ang ang equation ay magkakaroon lamang ng 1 ugat.

Sagot:

\(a\sa \kaliwa\(-\dfrac(18)(41);\dfrac(18)(23)\kanan\)\)

Gawain 4 #3072

Antas ng gawain: Katumbas sa Pinag-isang Pagsusulit ng Estado

Hanapin ang lahat ng mga halaga ng \(a\) , para sa bawat isa kung saan ang equation \

may hindi bababa sa isang ugat.

(Gawain mula sa mga subscriber)

Isulat muli natin ang equation sa anyo \ at isaalang-alang ang dalawang function: \(g(x)=7\sqrt(2x^2+49)\) at \(f(x)=3|x-7a|-6|x|-a^2+7a\ ).
Ang function na \(g(x)\) ay pantay at may pinakamababang punto \(x=0\) (at \(g(0)=49\) ).
Ang function na \(f(x)\) para sa \(x>0\) ay bumababa, at para sa \(x<0\) – возрастающей, следовательно, \(x=0\) – точка максимума.
Sa katunayan, kapag ang \(x>0\) ang pangalawang module ay magbubukas nang positibo (\(|x|=x\) ), samakatuwid, anuman ang pagbubukas ng unang module, ang \(f(x)\) ay magiging pantay sa \( kx+A\) , kung saan ang \(A\) ay ang expression ng \(a\) at ang \(k\) ay katumbas ng alinman sa \(-9\) o \(-3\) . Kapag \(x<0\) наоборот: второй модуль раскроется отрицательно и \(f(x)=kx+A\) , где \(k\) равно либо \(3\) , либо \(9\) .
Hanapin natin ang halaga ng \(f\) sa pinakamataas na punto: \

Upang ang equation ay magkaroon ng hindi bababa sa isang solusyon, kinakailangan na ang mga graph ng mga function \(f\) at \(g\) ay may kahit isang intersection point. Samakatuwid, kailangan mo: \ \\]

Sagot:

\(a\sa \(-7\)\cup\)

Gawain 5 #3912

Antas ng gawain: Katumbas sa Pinag-isang Pagsusulit ng Estado

Hanapin ang lahat ng mga halaga ng parameter \(a\) , para sa bawat isa kung saan ang equation \

ay may anim na magkakaibang solusyon.

Gawin natin ang kapalit na \((\sqrt2)^(x^3-3x^2+4)=t\) , \(t>0\) . Pagkatapos ang equation ay kukuha ng form \ Unti-unti nating isusulat ang mga kondisyon kung saan magkakaroon ng anim na solusyon ang orihinal na equation.
Tandaan na ang quadratic equation \((*)\) ay maaaring magkaroon ng maximum na dalawang solusyon. Anumang cubic equation \(Ax^3+Bx^2+Cx+D=0\) ay maaaring magkaroon ng hindi hihigit sa tatlong solusyon. Samakatuwid, kung ang equation na \((*)\) ay may dalawang magkaibang solusyon (positibo!, dahil ang \(t\) ay dapat na mas malaki kaysa sa zero) \(t_1\) at \(t_2\) , kung gayon, sa pamamagitan ng paggawa ng reverse pagpapalit, nakukuha namin: \[\left[\begin(gathered)\begin(aligned) &(\sqrt2)^(x^3-3x^2+4)=t_1\\ &(\sqrt2)^(x^3-3x^2 +4)=t_2\end(aligned)\end(gathered)\right.\] Dahil ang anumang positibong numero ay maaaring katawanin bilang \(\sqrt2\) sa ilang lawak, halimbawa, \(t_1=(\sqrt2)^(\log_(\sqrt2) t_1)\), pagkatapos ang unang equation ng set ay muling isusulat sa form \ Tulad ng nasabi na natin, ang anumang cubic equation ay hindi hihigit sa tatlong solusyon, samakatuwid, ang bawat equation sa set ay magkakaroon ng hindi hihigit sa tatlong solusyon. Nangangahulugan ito na ang buong set ay magkakaroon ng hindi hihigit sa anim na solusyon.
Nangangahulugan ito na para sa orihinal na equation na magkaroon ng anim na solusyon, ang quadratic equation \((*)\) ay dapat may dalawang magkaibang solusyon, at ang bawat resultang cubic equation (mula sa set) ay dapat magkaroon ng tatlong magkakaibang solusyon (at hindi isang solong solusyon ng ang isang equation ay dapat tumugma sa alinman -sa pamamagitan ng desisyon ng pangalawa!)
Malinaw, kung ang quadratic equation \((*)\) ay may isang solusyon, hindi tayo makakakuha ng anim na solusyon sa orihinal na equation.

Kaya, ang plano ng solusyon ay nagiging malinaw. Isulat natin ang mga kundisyon na dapat matugunan sa bawat punto.

1) Para ang equation na \((*)\) ay magkaroon ng dalawang magkaibang solusyon, ang discriminant nito ay dapat na positibo: \

2) Kinakailangan din na ang parehong mga ugat ay positibo (dahil \(t>0\) ). Kung ang produkto ng dalawang ugat ay positibo at ang kanilang kabuuan ay positibo, kung gayon ang mga ugat mismo ay magiging positibo. Samakatuwid, kailangan mo: \[\begin(cases) 12-a>0\\-(a-10)>0\end(cases)\quad\Leftrightarrow\quad a<10\]

Kaya, nabigyan na natin ang ating sarili ng dalawang magkaibang positibong ugat \(t_1\) at \(t_2\) .

3) Tingnan natin ang equation na ito \ Para sa ano \(t\) magkakaroon ito ng tatlong magkakaibang solusyon?
Isaalang-alang ang function na \(f(x)=x^3-3x^2+4\) .
Maaaring i-factorize: \ Samakatuwid, ang mga zero nito ay: \(x=-1;2\) .
Kung nahanap natin ang derivative \(f"(x)=3x^2-6x\) , pagkatapos ay makakakuha tayo ng dalawang extremum point \(x_(max)=0, x_(min)=2\) .
Samakatuwid, ang graph ay ganito ang hitsura:


Nakikita namin na ang anumang pahalang na linya \(y=k\) , kung saan \(0 \(x^3-3x^2+4=\log_(\sqrt2) t\) nagkaroon ng tatlong magkakaibang solusyon, kinakailangan na \(0<\log_ {\sqrt2}t<4\) .
Kaya, kailangan mo: \[\begin(cases) 0<\log_{\sqrt2}t_1<4\\ 0<\log_{\sqrt2}t_2<4\end{cases}\qquad (**)\] Agad din nating tandaan na kung magkaiba ang mga numerong \(t_1\) at \(t_2\), ang mga numerong \(\log_(\sqrt2)t_1\) at \(\log_(\sqrt2)t_2\) ay magiging naiiba, na nangangahulugang ang mga equation \(x^3-3x^2+4=\log_(\sqrt2) t_1\) At \(x^3-3x^2+4=\log_(\sqrt2) t_2\) magkakaroon ng magkakaibang ugat.
Ang system \((**)\) ay maaaring muling isulat tulad ng sumusunod: \[\begin(cases) 1

Kaya, natukoy namin na ang parehong mga ugat ng equation \((*)\) ay dapat nasa pagitan ng \((1;4)\) . Paano isulat ang kundisyong ito?
Hindi namin isusulat nang tahasan ang mga ugat.
Isaalang-alang ang function na \(g(t)=t^2+(a-10)t+12-a\) . Ang graph nito ay isang parabola na may mga pataas na sanga, na may dalawang punto ng intersection sa x-axis (isinulat namin ang kundisyong ito sa talata 1)). Ano ang dapat na hitsura ng graph nito upang ang mga punto ng intersection sa x-axis ay nasa pagitan ng \((1;4)\)? Kaya:


Una, ang mga halaga \(g(1)\) at \(g(4)\) ng function sa mga puntong \(1\) at \(4\) ay dapat na positibo, at pangalawa, ang vertex ng Ang parabola \(t_0\ ) ay dapat ding nasa pagitan ng \((1;4)\) . Samakatuwid, maaari naming isulat ang system: \[\begin(cases) 1+a-10+12-a>0\\ 4^2+(a-10)\cdot 4+12-a>0\\ 1<\dfrac{-(a-10)}2<4\end{cases}\quad\Leftrightarrow\quad 4 Ang \(a\) ay laging may kahit isang ugat \(x=0\) . Nangangahulugan ito na upang matupad ang mga kondisyon ng problema ay kinakailangan na ang equation \

ay may apat na magkakaibang ugat, naiiba sa zero, na kumakatawan, kasama ng \(x=0\), isang pag-unlad ng aritmetika.

Tandaan na ang function na \(y=25x^4+25(a-1)x^2-4(a-7)\) ay pantay, na nangangahulugan na kung ang \(x_0\) ay ang ugat ng equation \( (*)\ ) , pagkatapos ay \(-x_0\) din ang magiging ugat nito. Pagkatapos ay kinakailangan na ang mga ugat ng equation na ito ay mga numerong inayos sa pataas na pagkakasunud-sunod: \(-2d, -d, d, 2d\) (pagkatapos ay \(d>0\)). Pagkatapos ang limang numerong ito ay bubuo ng isang pag-unlad ng aritmetika (na may pagkakaibang \(d\)).

Upang ang mga ugat na ito ay maging mga numero \(-2d, -d, d, 2d\) , kinakailangan na ang mga numerong \(d^(\,2), 4d^(\,2)\) ay ang mga ugat ng ang equation \(25t^2 +25(a-1)t-4(a-7)=0\) . Pagkatapos, ayon sa teorama ni Vieta:

Isulat muli natin ang equation sa anyo \ at isaalang-alang ang dalawang function: \(g(x)=20a-a^2-2^(x^2+2)\) at \(f(x)=13|x|-2|5x+12a|\) .
Ang function na \(g(x)\) ay may pinakamataas na punto \(x=0\) (at \(g_(\text(itaas))=g(0)=-a^2+20a-4\)):
\(g"(x)=-2^(x^2+2)\cdot \ln 2\cdot 2x\). Zero derivative: \(x=0\) . Kapag \(x<0\) имеем: \(g">0\) , para sa \(x>0\) : \(g"<0\) .
Ang function na \(f(x)\) para sa \(x>0\) ay tumataas, at para sa \(x<0\) – убывающей, следовательно, \(x=0\) – точка минимума.
Sa katunayan, kapag ang \(x>0\) ang unang module ay magbubukas nang positibo (\(|x|=x\)), samakatuwid, anuman ang pagbubukas ng pangalawang module, ang \(f(x)\) ay magiging katumbas sa \( kx+A\) , kung saan ang \(A\) ay ang expression ng \(a\) , at ang \(k\) ay katumbas ng alinman sa \(13-10=3\) o \(13+10 =23\) . Kapag \(x<0\) наоборот: первый модуль раскроется отрицательно и \(f(x)=kx+A\) , где \(k\) равно либо \(-3\) , либо \(-23\) .
Hanapin natin ang halaga ng \(f\) sa pinakamababang punto: \

Upang ang equation ay magkaroon ng hindi bababa sa isang solusyon, kinakailangan na ang mga graph ng mga function \(f\) at \(g\) ay may kahit isang intersection point. Samakatuwid, kailangan mo: \ Ang paglutas ng hanay ng mga sistemang ito, makukuha natin ang sagot: \\]

Sagot:

\(a\sa \(-2\)\cup\)

Ang pag-asa ng isang variable na y sa isang variable na x, kung saan ang bawat halaga ng x ay tumutugma sa isang solong halaga ng y ay tinatawag na isang function. Para sa pagtatalaga gamitin ang notasyon y=f(x). Ang bawat function ay may ilang pangunahing katangian, tulad ng monotonicity, parity, periodicity at iba pa.

Tingnang mabuti ang parity property.

Tinatawag ang isang function na y=f(x) kahit na natutugunan nito ang sumusunod na dalawang kundisyon:

2. Ang value ng function sa point x, na kabilang sa domain ng definition ng function, ay dapat na katumbas ng value ng function sa point -x. Iyon ay, para sa anumang punto x, mula sa domain ng kahulugan ng function ang sumusunod na pagkakapantay-pantay ay dapat masiyahan: f(x) = f(-x).

Graph ng pantay na function

Kung mag-plot ka ng graph ng pantay na function, ito ay magiging simetriko tungkol sa Oy axis.

Halimbawa, ang function na y=x^2 ay pantay. Tingnan natin ito. Ang domain ng kahulugan ay ang buong numerical axis, na nangangahulugang ito ay simetriko tungkol sa punto O.

Kumuha tayo ng arbitraryong x=3. f(x)=3^2=9.

f(-x)=(-3)^2=9. Samakatuwid f(x) = f(-x). Kaya, ang parehong mga kondisyon ay natutugunan, na nangangahulugang ang pag-andar ay pantay. Nasa ibaba ang isang graph ng function na y=x^2.

Ipinapakita ng figure na ang graph ay simetriko tungkol sa Oy axis.

Graph ng isang kakaibang function

Ang isang function na y=f(x) ay tinatawag na kakaiba kung natutugunan nito ang sumusunod na dalawang kundisyon:

1. Ang domain ng kahulugan ng isang ibinigay na function ay dapat na simetriko na may paggalang sa point O. Iyon ay, kung ang ilang punto a ay kabilang sa domain ng kahulugan ng function, kung gayon ang kaukulang punto -a ay dapat ding kabilang sa domain ng kahulugan ng ibinigay na function.

2. Para sa anumang puntong x, ang sumusunod na pagkakapantay-pantay ay dapat masiyahan mula sa domain ng kahulugan ng function: f(x) = -f(x).

Ang graph ng isang kakaibang function ay simetriko na may kinalaman sa punto O - ang pinagmulan ng mga coordinate. Halimbawa, ang function na y=x^3 ay kakaiba. Tingnan natin ito. Ang domain ng kahulugan ay ang buong numerical axis, na nangangahulugang ito ay simetriko tungkol sa punto O.

Kumuha tayo ng arbitrary x=2. f(x)=2^3=8.

f(-x)=(-2)^3=-8. Samakatuwid f(x) = -f(x). Kaya, ang parehong mga kondisyon ay natutugunan, na nangangahulugan na ang pag-andar ay kakaiba. Nasa ibaba ang isang graph ng function na y=x^3.

Ang figure ay malinaw na nagpapakita na ang kakaibang function y=x^3 ay simetriko tungkol sa pinagmulan.